debug64

Даны координаты центров окружностей и их радиусы. Необходимо найти точки пересечения этих окружностей.

Кликните на картинке, что бы посмотреть как это работает.

Точка P1 является центром первой окружности радиусом R1 и точка P2 центром второй окружности радиусом R2.

Обозначим:

• h - высота треугольника P1P3P2 (расстояние между точками P3 и P0)
• *a - расстояние между точками P1 и P0
• *b - расстояние между точками P2 и P0
• d = a + b; - расстояние между точками P1 и P2

Проверяем, если R1 + R2 < d, тогда окружности не пересекаются, т.к. лежат отдельно, если |R1 - R2| > d, тогда окружности так же не пересекаются, т.к. одна окружность находится внутри другой.

Рассмотрим 2 прямоугольных треугольника, P1P3P0 и P2P3P0. Получаем:

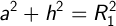
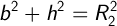
Так как эти треугольники имеют общий катет (h), тогда:

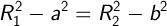
Выразим a через b:

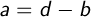
тогда,

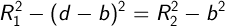
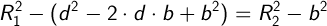
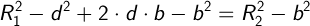
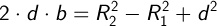
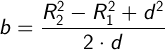
Зная b, находим а:

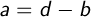
Найдем точку P0 с помощью векторного параметрического уравнения прямой:

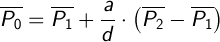
Зная координаты точки P0 находим координаты точек P3 и P4. Для этого возмем единичный вектор от P1 до P2, повернем его на +90 градусов для P3 (-90 градусов для P4) и умножим на h.

Таким образом находим координаты точки P3:

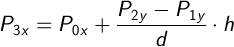
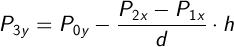
Аналогично находим координаты точки P4:

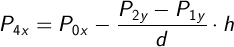
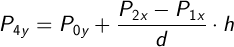
Реализацию этого способа вы найдете в исходном коде этой страницы, метод Circle.moGetCrossPoints

2й способ решения задачи.

Так как точки пересечения окружностей общие, тогда запишем уравнения окружностей в виде системы уранений:

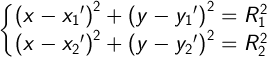
Для упрощения преобразований, переместим центр окружности 1 в начало координат и пересчитаем координаты центра второй окружности:

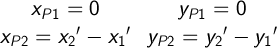
Перепишем систему уранений для новых координат:

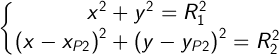
Раскроем скобки во втором уравнении:

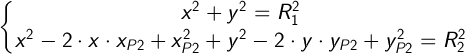
Вычтем из второго уравнения первое и перенесем известные в правую часть:

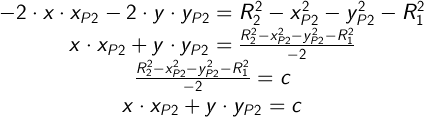
Выразим:

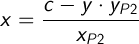
Если XP2 не равен 0, тогда подставляем X в уравнение первой окружности:

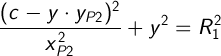
Раскрываем скобки и избавляемся от знаменателя:

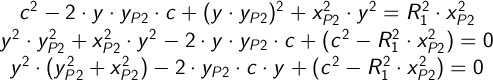
Как видим у нас получается квадратное уравнение, обозначим:

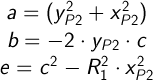
Тогда:

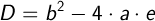
• Если D < 0, значит окружности не пересекаются
• Если D = 0, значит окружности соприкасаются и имееют одну точку пересечения
  
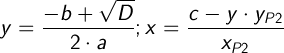
• Если D > 0, значит окружности пересекаются и имеют две точки пересечения
  

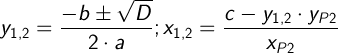
Если XP2 = 0, тогда решаем через Y и получаем:

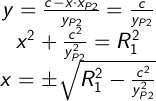
Помним, если под корнем число отрицательное, значит окружности не пересекаются, если равно 0, тогда окружности соприкасаются и имееют одну точку пересечения, если число больше 0, тогда X может быть как отрицательным, так и положительным.

Реализацию этого способа вы найдете в исходном коде этой страницы, метод Circle.moGetCrossPoints2