Расстояние от точки до отрезка/прямой

Wed Mar 01, 2017 by debug64 in math

Для вычисления расстояния от точки до прямой, необходимо опустить перпендикуляр из точки на это прямую. Это будет точка Р на прямой.

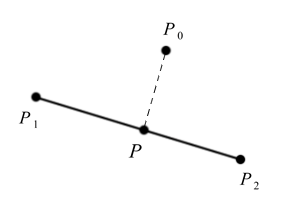
Нахождение точки P можно задать параметрическим образом:

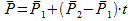
Так как отрезки P₁P₂ и P₀P перпендикулярны, то скалярное произведение между соответстующими векторами равно нулю 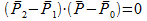. Делая подстановку, находим значение параметра t:

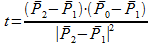
Если t < 0 или t > 1, то перпендикуляр лежит за пределами отрезка P₁P₂

Пример реализации на C++:

float getDistBetweenPointAndStraight(const Vector4& oPos, const Vector4& oPt1, const Vector4& oPt2)
{
	Vector4 oV21 = oPt2 - oPt1;
	Vector4 oV01 = oPos - oPt1;
	float е = oV21 * oV01 / oV21.length2();
	Vector4 oP = oPt1 + oV21 * е;
	float fDist = (oPos - oP).length();
	return fDist;
}

Пример Vector4:

class Vector4
{
public:

    float x, y, z, w;

    Vector4(void) {
        this->x=0; this->y=0; this->z=0; this->w=1;
    }

    Vector4(float x, float y, float z=0, float w=1) {
        this->x=x; this->y=y; this->z=z; this->w=w;
    }

    /// Сложение векторов
    inline Vector4 operator + (const Vector4& v) const {
        return Vector4(x+v.x, y+v.y,
            z+v.z, w/*+v.w*/);
    }

    /// Вычитание векторов
    inline Vector4 operator - (const Vector4& v) const {
        return Vector4(x-v.x, y-v.y,
            z-v.z, w );
    }

    /// Скалярное произведение
    inline float operator * (const Vector4& v) const {
        return x*v.x+y*v.y+z*v.z ;
    }

    /// Векторное произведение
    inline const Vector4 operator ^ (const Vector4& v) const {
        return Vector4(y*v.z-z*v.y,
            z*v.x-x*v.z ,
            x*v.y-y*v.x, 1);
    }

    /// Умножение вектора на число
    inline Vector4 operator * (float v) const {
        return Vector4(x*v, y*v, z*v, w);
    }

    /// Деление вектора на число
    inline Vector4 operator / (float v) const {
        return Vector4(x/v, y/v, z/v, w);
    }

    /// Negation operator. Returns the negative of the Vector4.
    inline const Vector4 operator - () const {
        return Vector4 (-x, -y, -z, /*-*/w);
    }

    /// Длина вектора
    inline float length() const {
        return sqrtf( x*x + y*y + z*z );
    }

    /// квадрат длины вектора
    inline float length2() const {
        return x*x + y*y + z*z;
    }
};