debug64

Один из вариантов решения задачи.

Треугольник A B C вписан в данную окружность. А как известно, центр вписанной окружности расположен в точке пересечения серединных перпендикуляров к сторонам треугольника.

Следовательно, для решения данной задачи необходимо:

• Найти координаты середины отрезка A B (пусть это будет точка P1) и составить уравнение серединного перпендикуляра к отрезку A B проходящего через точку P1.
• Тоже самое делаем для B C, находим координаты середины отрезка B C (пусть это будет точка P2) и составить уравнение серединного перпендикуляра к отрезку B C проходящего через точку P2.
• Найти координаты точки пересечения серединных перпендикуляров, решив соответствующую систему двух линейных уравнений.

Начинаем с уравнения прямой: A⋅x + B⋅y + C = 0
Зная две точки лежащие на этой прямой, A и B, подставляем их в уравнение:

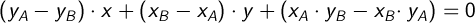
Аналогично для B и C:

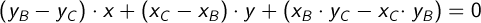
Уравнение прямой которая перпендикулярна
A⋅x + B⋅y + C = 0 выглядит так:
B⋅x - A⋅y + C2 = 0
Пример такого преобразования хорошо описан тут: Прикладная математика

Следовательно, уравнение перпендикуляра к отрезку A B проходящего через точку P1:

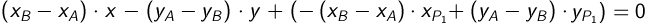
аналогично, уравнение перпендикуляра к отрезку B C проходящего через точку P2:

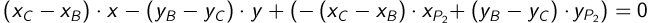
Эти прямые пересекаются в центре окружности. Таким образом мы получаем систему уравнений с двумя неизвестными:

Обзначим для простоты:

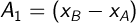
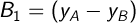
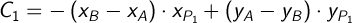
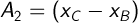
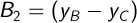
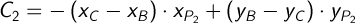
и составим систему уравнений:

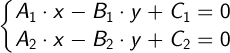
Варианты решения системы двух линейных уравнений с двумя неизвестными можно посмотреть тут:
Вся элементарная математика

Решая систему уравнений получим:

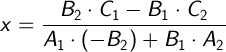
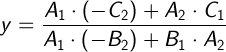
Посмотреть как это работает в реальном времени вы можете на картинке вверху страницы. Сделайте несколько кликов на картинке.

Кликните на картинке, что бы посмотреть как это работает в реальном времени

Уравнение прямой проходящей через A B

Уравнение прямой проходящей через B C